The Art of Making Multiple Images From a Matrix
An implementation of matrix multiplication in C# and its usage for basic image transformations similar rotation, stretching, flipping and colour density irresolute.
Introduction
Today, I volition show you my implementation of matrix multiplication C# and how to use information technology to utilize bones transformations to images like rotation, stretching, flipping, and modifying colour density.
Please annotation that this is not an image processing grade. Rather, this commodity demonstrates in C# 3 of the core linear algebra concepts, matrix multiplication, dot product, and transformation matrices.
Source Lawmaking
Source code for this article is available on GitHub on the following repository: https://github.com/elsheimy/Elsheimy.Samples.LinearTransformations
This implementation is besides included in the linear algebra bug component, Elsheimy.Components.Linears, available on:
- GitHub: https://github.com/elsheimy/Elsheimy.Components.Linears
- NuGet: https://www.nuget.org/packages/Elsheimy.Components.Linears
Matrix Multiplication
The math behind matrix multiplication is very straightforward. Very piece of cake explanations can be establish here and hither.
Let'southward get directly to the lawmaking and start with our main function:
public static double[,] Multiply(double[,] matrix1, double[,] matrix2) { var matrix1Rows = matrix1.GetLength(0); var matrix1Cols = matrix1.GetLength(one); var matrix2Rows = matrix2.GetLength(0); var matrix2Cols = matrix2.GetLength(1); if (matrix1Cols != matrix2Rows) throw new InvalidOperationException (" Product is undefined. n columns of starting time matrix must equal to north rows of 2nd matrix"); double[,] product = new double[matrix1Rows, matrix2Cols]; for (int matrix1_row = 0; matrix1_row < matrix1Rows; matrix1_row++) { for (int matrix2_col = 0; matrix2_col < matrix2Cols; matrix2_col++) { for (int matrix1_col = 0; matrix1_col < matrix1Cols; matrix1_col++) { product[matrix1_row, matrix2_col] += matrix1[matrix1_row, matrix1_col] * matrix2[matrix1_col, matrix2_col]; } } } return product; }
We started by fetching matrix row and column counts using Assortment.GetLength() and stored them inside variables to utilize them later. At that place's a performance hit when calling Assortment.GetLength() that's why we stored its results inside variables rather than calling the function multiple times. The performance part of this code is covered later in this commodity.
Next, we guaranteed that the production is defined past comparison the matrix1 number of columns to the matrix2 number of rows. An exception is thrown if the product is undefined.
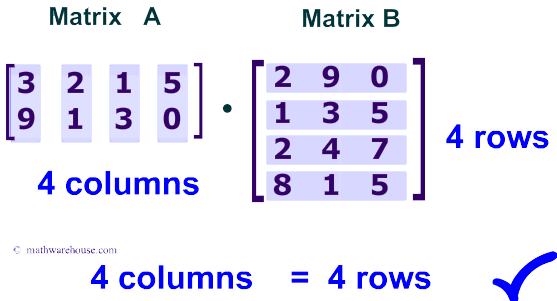
Photo Credit: MathwareHouse
Then we created the final product matrix using the row and column lengths of the original matrices.
After that, we used three loops to move through matrix vectors and to calculate the dot product.

Photograph Credit: PurpleMath
Transformations
At present nosotros can use our multiplication algorithm to create image transformation matrices that tin can exist applied to any point (X, Y) or color (ARGB) to modify it. Nosotros will get-go by defining our abstract IImageTransformation interface that has two members: CreateTransformationMatrix() and IsColorTransformation. The offset i returns the relevant transformation matrix, the 2nd indicates if this transformation can be applied to colors (truthful) or points (false).
public interface IImageTransformation { double[,] CreateTransformationMatrix(); bool IsColorTransformation { go; } }
Rotation Transformation
The 2d rotation matrix is divers as:

Photograph Credit: Academo
Our code is very clear:
public class RotationImageTransformation : IImageTransformation { public double AngleDegrees { become; set; } public double AngleRadians { get { return DegreesToRadians(AngleDegrees); } gear up { AngleDegrees = RadiansToDegrees(value); } } public bool IsColorTransformation { get { render imitation; } } public static double DegreesToRadians(double degree) { return caste * Math.PI / 180; } public static double RadiansToDegrees(double radians) { return radians / Math.PI * 180; } public double[,] CreateTransformationMatrix() { double[,] matrix = new double[two, 2]; matrix[0, 0] = Math.Cos(AngleRadians); matrix[ane, 0] = Math.Sin(AngleRadians); matrix[0, 1] = -one * Math.Sin(AngleRadians); matrix[i, 1] = Math.Cos(AngleRadians); return matrix; } public RotationImageTransformation() { } public RotationImageTransformation(double angleDegree) { this.AngleDegrees = angleDegree; } }
Equally you lot tin can see in this code, Sin() and Cos() accept angels in radians, that's why we have used ii extra functions to convert between radians and degrees to go along things simple to the user.
A very nice explanation and example of 2d rotation matrices is available here.
Stretching/Scaling Transformation
The second transformation we have is the cistron-scaling transformation. It works by scaling X/Y by the required factor. It is defined as:
public class StretchImageTransformation : IImageTransformation { public double HorizontalStretch { get; set up; } public double VerticalStretch { get; set up; } public bool IsColorTransformation { get { return faux; } } public double[,] CreateTransformationMatrix() { double[,] matrix = Matrices.CreateIdentityMatrix(2); matrix[0, 0] += HorizontalStretch; matrix[1, 1] += VerticalStretch; return matrix; } public StretchImageTransformation() { } public StretchImageTransformation(double horizStretch, double vertStretch) { this.HorizontalStretch = horizStretch; this.VerticalStretch = vertStretch; } }
Identity Matrix
The previous lawmaking requires the apply of an identity matrix. Hither's the code that defines CreateIdentityMatrix(),
public static double[,] CreateIdentityMatrix(int length) { double[,] matrix = new double[length, length]; for (int i = 0, j = 0; i < length; i++, j++) matrix[i, j] = i; return matrix; }
Flipping Transformation
The 3rd transformation nosotros have is the flipping transformation. It works by negating the X and Y members to flip the vector over the vertical and horizontal axis respectively.
public grade FlipImageTransformation : IImageTransformation { public bool FlipHorizontally { get; prepare; } public bool FlipVertically { get; set; } public bool IsColorTransformation { get { return false; } } public double[,] CreateTransformationMatrix() { double[,] matrix = Matrices.CreateIdentityMatrix(two); if (FlipHorizontally) matrix[0, 0] *= -ane; if (FlipVertically) matrix[i, 1] *= -one; return matrix; } public FlipImageTransformation() { } public FlipImageTransformation(bool flipHoriz, bool flipVert) { this.FlipHorizontally = flipHoriz; this.FlipVertically = flipVert; } }
Color Density Transformation
The final transformation we take is the color density transformation. It works by defining different scaling factors to color components (Alpha, Red, Green, and Blueish). For example, if you want to make the color fifty% transparent we would scale Alpha by 0.5. If yous want to remove the Red color completely you could scale it by 0. And so on.
public class DensityImageTransformation : IImageTransformation { public double AlphaDensity { get; set; } public double RedDensity { get; prepare; } public double GreenDensity { get; fix; } public double BlueDensity { get; set; } public bool IsColorTransformation { get { return true; } } public double[,] CreateTransformationMatrix() { double[,] matrix = new double[,]{ { AlphaDensity, 0, 0, 0}, { 0, RedDensity, 0, 0}, { 0, 0, GreenDensity, 0}, { 0, 0, 0, BlueDensity}, }; render matrix; } public DensityImageTransformation() { } public DensityImageTransformation(double alphaDensity, double redDensity, double greenDensity, double blueDensity) { this.AlphaDensity = alphaDensity; this.RedDensity = redDensity; this.GreenDensity = greenDensity; this.BlueDensity = blueDensity; } }
Connecting Things Together
Now it is time to define the processes and procedures that connect things together. Here'south the full code. An explanation follows:
public static Bitmap Apply(string file, IImageTransformation[] transformations) { using (Bitmap bmp = (Bitmap)Bitmap.FromFile(file)) { return Apply(bmp, transformations); } } public static Bitmap Use(Bitmap bmp, IImageTransformation[] transformations) { PointColor[] points = new PointColor[bmp.Width * bmp.Height]; var pointTransformations = transformations.Where(s => southward.IsColorTransformation == false).ToArray(); var colorTransformations = transformations.Where(s => due south.IsColorTransformation == true).ToArray(); double[,] pointTransMatrix = CreateTransformationMatrix(pointTransformations, ii); double[,] colorTransMatrix = CreateTransformationMatrix(colorTransformations, 4); int minX = 0, minY = 0; int maxX = 0, maxY = 0; int idx = 0; for (int x = 0; x < bmp.Width; ten++) { for (int y = 0; y < bmp.Height; y++) { var production = Matrices.Multiply(pointTransMatrix, new double[,] { { x }, { y } }); var newX = (int)product[0, 0]; var newY = (int)product[1, 0]; minX = Math.Min(minX, newX); minY = Math.Min(minY, newY); maxX = Math.Max(maxX, newX); maxY = Math.Max(maxY, newY); Colour clr = bmp.GetPixel(x, y); var colorProduct = Matrices.Multiply( colorTransMatrix, new double[,] { { clr.A }, { clr.R }, { clr.G }, { clr.B } }); clr = Color.FromArgb( GetValidColorComponent(colorProduct[0, 0]), GetValidColorComponent(colorProduct[1, 0]), GetValidColorComponent(colorProduct[two, 0]), GetValidColorComponent(colorProduct[3, 0]) ); points[idx] = new PointColor() { X = newX, Y = newY, Color = clr }; idx++; } } var width = maxX - minX + i; var superlative = maxY - minY + 1; var img = new Bitmap(width, height); foreach (var pnt in points) img.SetPixel( pnt.X - minX, pnt.Y - minY, pnt.Colour); return img; } private static byte GetValidColorComponent(double c) { c = Math.Max(byte.MinValue, c); c = Math.Min(byte.MaxValue, c); return (byte)c; } individual static double[,] CreateTransformationMatrix (IImageTransformation[] vectorTransformations, int dimensions) { double[,] vectorTransMatrix = Matrices.CreateIdentityMatrix(dimensions); foreach (var trans in vectorTransformations) vectorTransMatrix = Matrices.Multiply(vectorTransMatrix, trans.CreateTransformationMatrix()); return vectorTransMatrix; }
We started past defining two overloads of Apply() part. 1 that accepts image file name and transformation listing and the other accepts a Bitmap object and the transformation listing to apply to that prototype.
Within the Apply() part, we filtered transformations into two groups, those that work on betoken locations (X and Y) and those that work on colors. Nosotros also used the CreateTransformationMatrix() role for each grouping to combine the transformations into a single transformation matrix.
After that, we started scanning the image and applying the transformations to points and colors respectively. Notice that we had to ensure that the transformed color components are byte-sized. Subsequently applying the transformations we saved information in an array for later on usage.
During the scanning process, we recorded our minimum and maximum Ten and Y values. This will help to set the new image size and shift the points as needed. Some transformations like stretching might increase or decrease paradigm size.
Finally, we created the new Bitmap object and set the bespeak data after shifting them.
Creating the Client
Our client awarding is simple. Here's a screenshot of our form,

Let's have a expect at the code behind information technology:
private string _file; individual Stopwatch _stopwatch; public ImageTransformationsForm() { InitializeComponent(); } individual void BrowseButton_Click(object sender, EventArgs e) { cord file = OpenFile(); if (file != goose egg) { this.FileTextBox.Text = file; _file = file; } } public static string OpenFile() { OpenFileDialog dlg = new OpenFileDialog(); dlg.CheckFileExists = true; if (dlg.ShowDialog() == DialogResult.OK) return dlg.FileName; return null; } individual void ApplyButton_Click(object sender, EventArgs due east) { if (_file == cipher) return; DisposePreviousImage(); RotationImageTransformation rotation = new RotationImageTransformation((double)this.AngleNumericUpDown.Value); StretchImageTransformation stretch = new StretchImageTransformation( (double)this.HorizStretchNumericUpDown.Value / 100, (double)this.VertStretchNumericUpDown.Value / 100); FlipImageTransformation flip = new FlipImageTransformation(this.FlipHorizontalCheckBox.Checked, this.FlipVerticalCheckBox.Checked); DensityImageTransformation density = new DensityImageTransformation( (double)this.AlphaNumericUpDown.Value / 100, (double)this.RedNumericUpDown.Value / 100, (double)this.GreenNumericUpDown.Value / 100, (double)this.BlueNumericUpDown.Value / 100 ); StartStopwatch(); var bmp = ImageTransformer.Use(_file, new IImageTransformation[] { rotation, stretch, flip, density }); StopStopwatch(); this.ImagePictureBox.Image = bmp; } individual void StartStopwatch() { if (_stopwatch == zippo) _stopwatch = new Stopwatch(); else _stopwatch.Reset(); _stopwatch.Start(); } private void StopStopwatch() { _stopwatch.Stop(); this.ExecutionTimeLabel.Text = $" Full execution time is {_stopwatch.ElapsedMilliseconds} milliseconds"; } private void DisposePreviousImage() { if (this.ImagePictureBox.Image != null) { var tmpImg = this.ImagePictureBox.Paradigm; this.ImagePictureBox.Image = naught; tmpImg.Dispose(); } }
The lawmaking is straightforward. The only affair to mention is that information technology has e'er been a good practice to call Dispose() on disposable objects to ensure all-time performance.
Performance Notes
In our cadre Multiply() method, we mentioned that calling Array.GetLength() involves a huge functioning impact. I tried to cheque the logic behind Array.GetLength() with no success. The method is natively implemented, and I could non view its code using common disassembly tools. However, past benchmarking the two scenarios (code with a agglomeration of calls to Array.GetLength() and another lawmaking with only a single call to the same function) I found that the single telephone call lawmaking is 2x faster than the other.
Some other way to improve the functioning of our Multiply() method is to use dangerous code. Past accessing array contents straight you achieve superior processing performance.
Here's our new and updatedunsafe code:
public static double[,] MultiplyUnsafe(double[,] matrix1, double[,] matrix2) { var matrix1Rows = matrix1.GetLength(0); var matrix1Cols = matrix1.GetLength(1); var matrix2Rows = matrix2.GetLength(0); var matrix2Cols = matrix2.GetLength(1); if (matrix1Cols != matrix2Rows) throw new InvalidOperationException (" Product is undefined. n columns of showtime matrix must equal to due north rows of second matrix"); double[,] product = new double[matrix1Rows, matrix2Cols]; unsafe { fixed ( double* pProduct = product, pMatrix1 = matrix1, pMatrix2 = matrix2) { int i = 0; for (int matrix1_row = 0; matrix1_row < matrix1Rows; matrix1_row++) { for (int matrix2_col = 0; matrix2_col < matrix2Cols; matrix2_col++) { for (int matrix1_col = 0; matrix1_col < matrix1Cols; matrix1_col++) { var val1 = *(pMatrix1 + (matrix1Rows * matrix1_row) + matrix1_col); var val2 = *(pMatrix2 + (matrix2Cols * matrix1_col) + matrix2_col); *(pProduct + i) += val1 * val2; } i++; } } } } return product; }
Dangerous code will not compile unless you enable it from the Build tab in the Project Settings page.
The following effigy shows the difference betwixt the iii Multiply() scenarios when multiplying the 1000x1000 matrix by itself. The tests ran on mydying Core i5-2430M@2.4GHz 6GB RAM 1GB Intel Graphics laptop.
 I am not covering whatsoever performance improvements in the client or the Apply() method every bit it is not the core focus of the article.
I am not covering whatsoever performance improvements in the client or the Apply() method every bit it is not the core focus of the article.
Conclusion
This was my implementation of matrix multiplication. Feel free to send me your feedback and comments over the code and to update information technology every bit needed.
douglaspethilkiled.blogspot.com
Source: https://www.codeproject.com/Articles/5298657/Matrix-Multiplication-in-Csharp-Applying-Transform
0 Response to "The Art of Making Multiple Images From a Matrix"
Post a Comment