People Go to Family Garage Math Ixl Math Graph

Discrete Mathematics - More On Graphs

---

Graph Coloring

Graph coloring is the procedure of assignment of colors to each vertex of a graph Chiliad such that no next vertices get same color. The objective is to minimize the number of colors while coloring a graph. The smallest number of colors required to colour a graph 1000 is chosen its chromatic number of that graph. Graph coloring trouble is a NP Complete problem.

Method to Color a Graph

The steps required to color a graph Thou with due north number of vertices are as follows −

Footstep 1 − Arrange the vertices of the graph in some lodge.

Stride 2 − Choose the commencement vertex and color information technology with the outset color.

Stride 3 − Cull the next vertex and color information technology with the lowest numbered color that has not been colored on whatever vertices next to it. If all the adjacent vertices are colored with this color, assign a new colour to it. Echo this step until all the vertices are colored.

Case

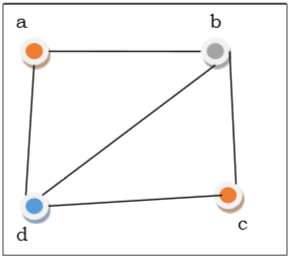
In the above figure, at first vertex $a$ is colored crimson. Equally the side by side vertices of vertex a are again adjacent, vertex $b$ and vertex $d$ are colored with unlike color, greenish and blueish respectively. Then vertex $c$ is colored as red as no adjacent vertex of $c$ is colored cerise. Hence, we could color the graph by 3 colors. Hence, the chromatic number of the graph is 3.

Applications of Graph Coloring

Some applications of graph coloring include −

• Register Resource allotment
• Map Coloring
• Bipartite Graph Checking
• Mobile Radio Frequency Consignment
• Making time tabular array, etc.

Graph Traversal

Graph traversal is the problem of visiting all the vertices of a graph in some systematic order. There are mainly two ways to traverse a graph.

• Breadth First Search
• Depth First Search

Breadth Outset Search

Breadth First Search (BFS) starts at starting level-0 vertex $X$ of the graph $G$. And so we visit all the vertices that are the neighbors of $X$. After visiting, we mark the vertices as "visited," and place them into level-i. And so we kickoff from the level-1 vertices and apply the aforementioned method on every level-1 vertex and so on. The BFS traversal terminates when every vertex of the graph has been visited.

BFS Algorithm

The concept is to visit all the neighbor vertices earlier visiting other neighbor vertices of neighbor vertices.

• Initialize status of all nodes as "Ready".

• Put source vertex in a queue and change its status to "Waiting".

• Repeat the following 2 steps until queue is empty −

  • Remove the get-go vertex from the queue and mark information technology as "Visited".

  • Add together to the rear of queue all neighbors of the removed vertex whose status is "Ready". Marker their status as "Waiting".

Problem

Let us take a graph (Source vertex is 'a') and use the BFS algorithm to notice out the traversal order.

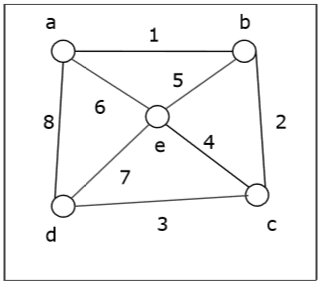
Solution −

• Initialize status of all vertices to "Gear up".

• Put a in queue and change its status to "Waiting".

• Remove a from queue, marker it equally "Visited".

• Add a's neighbors in "Ready" state b, d and e to end of queue and mark them as "Waiting".

• Remove b from queue, mark it as "Visited", put its "Gear up" neighbor c at end of queue and mark c equally "Waiting".

• Remove d from queue and marker it as "Visited". It has no neighbor in "Prepare" land.

• Remove due east from queue and mark it as "Visited". It has no neighbor in "Set up" state.

• Remove c from queue and mark it equally "Visited". It has no neighbor in "Set up" country.

• Queue is empty and then stop.

So the traversal order is −

$a \rightarrow b \rightarrow d \rightarrow e \rightarrow c$

The alternate orders of traversal are −

$a \rightarrow b \rightarrow e \rightarrow d \rightarrow c$

Or, $a \rightarrow d \rightarrow b \rightarrow e \rightarrow c$

Or, $a \rightarrow e \rightarrow b \rightarrow d \rightarrow c$

Or, $a \rightarrow b \rightarrow e \rightarrow d \rightarrow c$

Or, $a \rightarrow d \rightarrow e \rightarrow b \rightarrow c$

Application of BFS

• Finding the shortest path
• Minimum spanning tree for united nations-weighted graph
• GPS navigation system
• Detecting cycles in an undirected graph
• Finding all nodes within 1 connected component

Complexity Assay

Let $G(V, E)$ exist a graph with $|V|$ number of vertices and $|East|$ number of edges. If latitude starting time search algorithm visits every vertex in the graph and checks every edge, then its time complexity would exist −

$$O( | V | + | E | ). O( | E | )$$

Information technology may vary between $O(1)$ and $O(|V2|)$

Depth Offset Search

Depth Offset Search (DFS) algorithm starts from a vertex $5$, then it traverses to its adjacent vertex (say x) that has not been visited earlier and mark as "visited" and goes on with the adjacent vertex of $ten$ and then on.

If at any vertex, information technology encounters that all the adjacent vertices are visited, so it backtracks until it finds the start vertex having an adjacent vertex that has not been traversed earlier. Then, it traverses that vertex, continues with its adjacent vertices until it traverses all visited vertices and has to backtrack again. In this manner, it will traverse all the vertices reachable from the initial vertex $v$.

DFS Algorithm

The concept is to visit all the neighbor vertices of a neighbor vertex before visiting the other neighbor vertices.

• Initialize status of all nodes as "Ready"

• Put source vertex in a stack and change its status to "Waiting"

• Repeat the post-obit 2 steps until stack is empty −

  • Popular the tiptop vertex from the stack and mark it as "Visited"

  • Push onto the top of the stack all neighbors of the removed vertex whose condition is "Ready". Mark their status equally "Waiting".

Problem

Allow u.s.a. accept a graph (Source vertex is 'a') and apply the DFS algorithm to find out the traversal order.

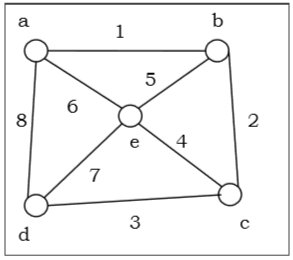
Solution

• Initialize status of all vertices to "Ready".

• Push button a in stack and alter its status to "Waiting".

• Pop a and mark it as "Visited".

• Button a's neighbors in "Set up" land due east, d and b to top of stack and mark them as "Waiting".

• Pop b from stack, mark information technology as "Visited", button its "Prepare" neighbour c onto stack.

• Pop c from stack and mark it as "Visited". Information technology has no "Ready" neighbor.

• Popular d from stack and mark information technology as "Visited". It has no "Prepare" neighbour.

• Pop e from stack and mark it as "Visited". It has no "Ready" neighbor.

• Stack is empty. So stop.

So the traversal society is −

$a \rightarrow b \rightarrow c \rightarrow d \rightarrow e$

The alternate orders of traversal are −

$a \rightarrow e \rightarrow b \rightarrow c \rightarrow d$

Or, $a \rightarrow b \rightarrow due east \rightarrow c \rightarrow d$

Or, $a \rightarrow d \rightarrow eastward \rightarrow b \rightarrow c$

Or, $a \rightarrow d \rightarrow c \rightarrow east \rightarrow b$

Or, $a \rightarrow d \rightarrow c \rightarrow b \rightarrow due east$

Complexity Analysis

Let $1000(Five, Eastward)$ be a graph with $|V|$ number of vertices and $|East|$ number of edges. If DFS algorithm visits every vertex in the graph and checks every edge, then the time complexity is −

$$\circleddash ( | V | + | E | )$$

Applications

• Detecting cycle in a graph
• To discover topological sorting
• To exam if a graph is bipartite
• Finding connected components
• Finding the bridges of a graph
• Finding bi-connectivity in graphs
• Solving the Knight's Tour problem
• Solving puzzles with only one solution

Useful Video Courses

---

Video

douglaspethilkiled.blogspot.com

Source: https://www.tutorialspoint.com/discrete_mathematics/more_on_graphs.htm

Share this post